Hi ha nombres que no es poden descompondre en producte de diversos factors i que es diuen primers, com per exemple el 97.
Hi ha nombres que es poden expressar com a producte de factors i que es diuen compostos. Un exemple seria 21 = 3 x 7.
Nombres més grans són difícils de descompondre.
11111 = 41 X 271
El nombre 1 no és compost però tampoc es considera un nombre primer.
El nombre 2 és el primer nombre primer i és l’únic primer parell.
El nombre 3 és el segon nombre primer.
El nombre 5 és el tercer nombre primer i és l’únic acabat en 5.
Tota la resta de primers han d’acabar en 1, 3, 7 o 9.
Els nombres primers només tenen dos divisors, els compostos tenen més de dos divisors i el nombre 1 només en té 1.
Eratòstenes, que també va mesurar el radi de la Terra, va idear un mètode (garbell d’Eratòstenes) per trobar els nombres primers. Es tracta de eliminar de la llista de naturals els múltiples de 2, de 3, de 5, de 7, etc.
Els nombres primers menors que 1000 són:
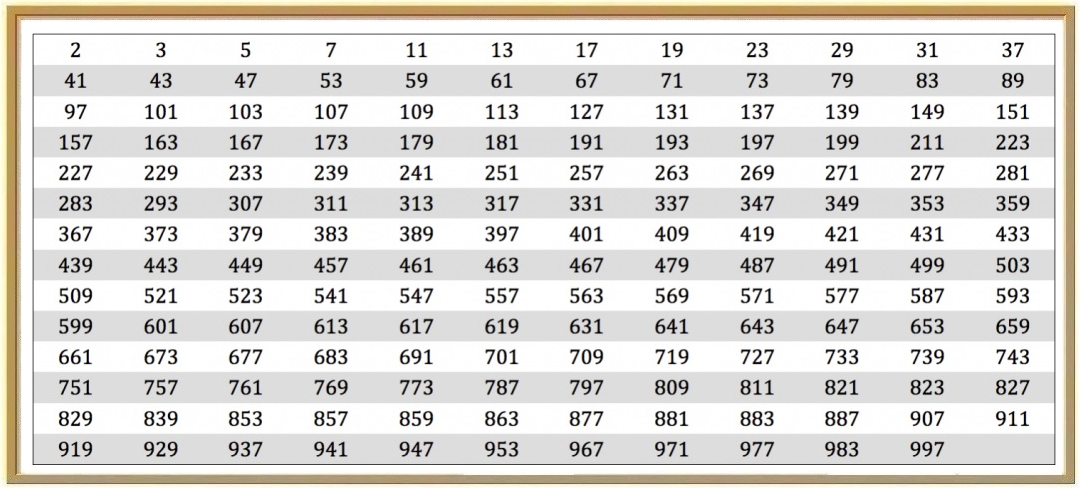
La distribució dels nombres primers és molt irregular i cada vegada en trobam més pocs. Entre 1 i 100 en trobam 25, però entre 901 i 1000 només en trobam 13 i entre 14901 i 15000 només 8.
Podríem pensar que arribaríem a un darrer nombre primer, però Euclides, al llibre novè dels Elements, ja va demostrar que hi ha infinits nombres primers.
Si agafam tots els primers coneguts (per exemple fins a 19) els multiplicam tots i sumam 1 obtindrem un nombre (exemple 2 · 3 · 5 · 7 · 11 · 13 · 17 · 19 + 1 = 9 699 691). El nombre obtingut no serà divisible per cap dels nombres primers coneguts (fins a 19) i, per tant, o serà primer, o es podrà descompondre en nombres primers majors que el major primer conegut. En aquest exemple, 9 699 691 no és primer, però es pot descompondre ( 347 x 27953 ). Hem trobat dos primers majors que 19.
També es pot demostrar que podem trobar 1000 nombres seguits (o un milió) sense trobar cap nombre primer.
En principi pot semblar que els nombres primers només han de ser una curiositat matemàtica sense cap utilitat, però s’ha trobat utilitat per encriptació de missatges i sistemes de seguretat en la comunicació de missatges.
Multiplicant dos nombres primers (p i q) podem obtenir fàcilment un nombre gros N (d’unes 400 xifres, per exemple). El procediment contrari de descompondre un nombre gros N en factors primers (p i q) és molt difícil i podria necessitar anys de càlculs amb ordinador.
p · q = N
Un missatge es pot encriptar emprant el nombre N (públic), de manera que només pot ser desencriptat per la persona que coneix els seus factors primers (p i q).
